Similar Soils with Loafercreek • SOILmilaR

In this vignette we will use “real” NASIS data via the loafercreek data set.

The loafercreek dataset includes soils that are generally similar to Loafercreek series concept, and occur spatially within a mapunit where Loafercreek or related soil is a major component. These mapunits are currently used in the Calaveras, Tuolumne, Mariposa and Butte county areas of California.

loafercreek is a SoilProfileCollection object. This is a special data structure defined by the {aqp} (Algorithms for Quantitative Pedology) package intended for managing soil horizon data, representing various depths within a soil “profile”, along with “site-level” data that corresponds to the point location or profile in aggregate.

A variety of {aqp} functions are used to calculate site-level characteristics that are used in hierarchical clustering methods from {stats} and {cluster} as well as similar soils calculations available via the {SOILmilaR} package. Methods for visualizing clusters are provided by the {sharpshootR} package.

First we load the required packages and datasets.

library(SOILmilaR)
library(aqp)
#> This is aqp 2.0.3
library(soilDB)

data("loafercreek", package="soilDB")

set.seed(0)
spc <- loafercreek[sample(1:length(loafercreek), 20)]

## alternately, use NASIS data
# spc <- fetchNASIS()

To use your own NASIS data you can replace the spc object (a random subset of loafercreek) with a call to soilDB::fetchNASIS(). The loafercreek object is a sample dataset stored in the {soilDB} package; therefore it does not require a NASIS installation or account to use.

Next, we define some rating functions that can be used for generating variables that can be used in comparing soils and assessing overall similarity.

rate_taxpartsize <- function(x, ...) {
  dplyr::case_match(x,
                    c("sandy-skeletal") ~ 1,
                    c("sandy") ~ 2,
                    c("loamy", "coarse-loamy", "coarse-silty") ~ 3,
                    c("fine-loamy", "fine-silty") ~ 4,
                    c("clayey", "fine") ~ 5,
                    c("very-fine") ~ 6,
                    c("loamy-skeletal", "clayey-skeletal") ~ 7)
  
}

rate_depthclass <- function(x,
                            breaks = c(
                              `very shallow` = 25,
                              `shallow` = 50,
                              `moderately deep` = 100,
                              `deep` = 150,
                              `very deep` = 1e4
                            ),
                            ...) {
  res <- cut(x, c(0, breaks))
  factor(res, levels = levels(res), labels = names(breaks))
}

Here we use several {aqp} functions to estimate the particle size control section boundaries, the depth to a root-restrictive layer, and apply our rating functions to the depth and particle size class as populated in NASIS.

site(spc) <- estimatePSCS(spc)

# calculate soil depth
spc$dp <- minDepthOf(spc, pattern = "R|Cr|Cd|kk|m")[[aqp::horizonDepths(spc)[1]]]

s <- similar_soils(spc, list(dp = rate_depthclass,
                             taxpartsize = rate_taxpartsize))
#> comparing to dominant reference condition (`3.4` on 17 rows)

# transfer some ordinal ratings
spc$rd = s$dp # depth class
spc$rt = s$taxpartsize # particle size class

We also calculate the weighted average clay content (pc) and percent volume rock fragments (pf) in the particle size control section we calculated above with aqp::estimatePSCS()

# calculate some continuous quantities for PSCS, join to site data
site(spc) <- site(mutate_profile(trunc(spc, spc$pscs_top, spc$pscs_bottom),
  pc = weighted.mean(clay, hzdepb - hzdept, na.rm=T),
  pf = weighted.mean(total_frags_pct, hzdepb - hzdept, na.rm=T)
))[c("peiid", "pc", "pf")]

We will now build several models with increasing complexity of the input data.

# set up data frames for various clustering models
x0 <- subset(site(spc), select = c("taxpartsize", "rd"))
x1 <- subset(site(spc), select = c("rt", "rd"))
x2 <- subset(site(spc), select = c("pc", "pf", "rd"))
x3 <- subset(site(spc), select = c("pc", "pf", "dp"))
x4 <- subset(site(spc), select = c("rt", "rd", "pc", "pf", "dp"))

The simplest model we construct uses the particle size family and the depth class.

m0 <- cluster::agnes(x0[complete.cases(x0),], method = "gaverage")
plot(as.dendrogram(m0))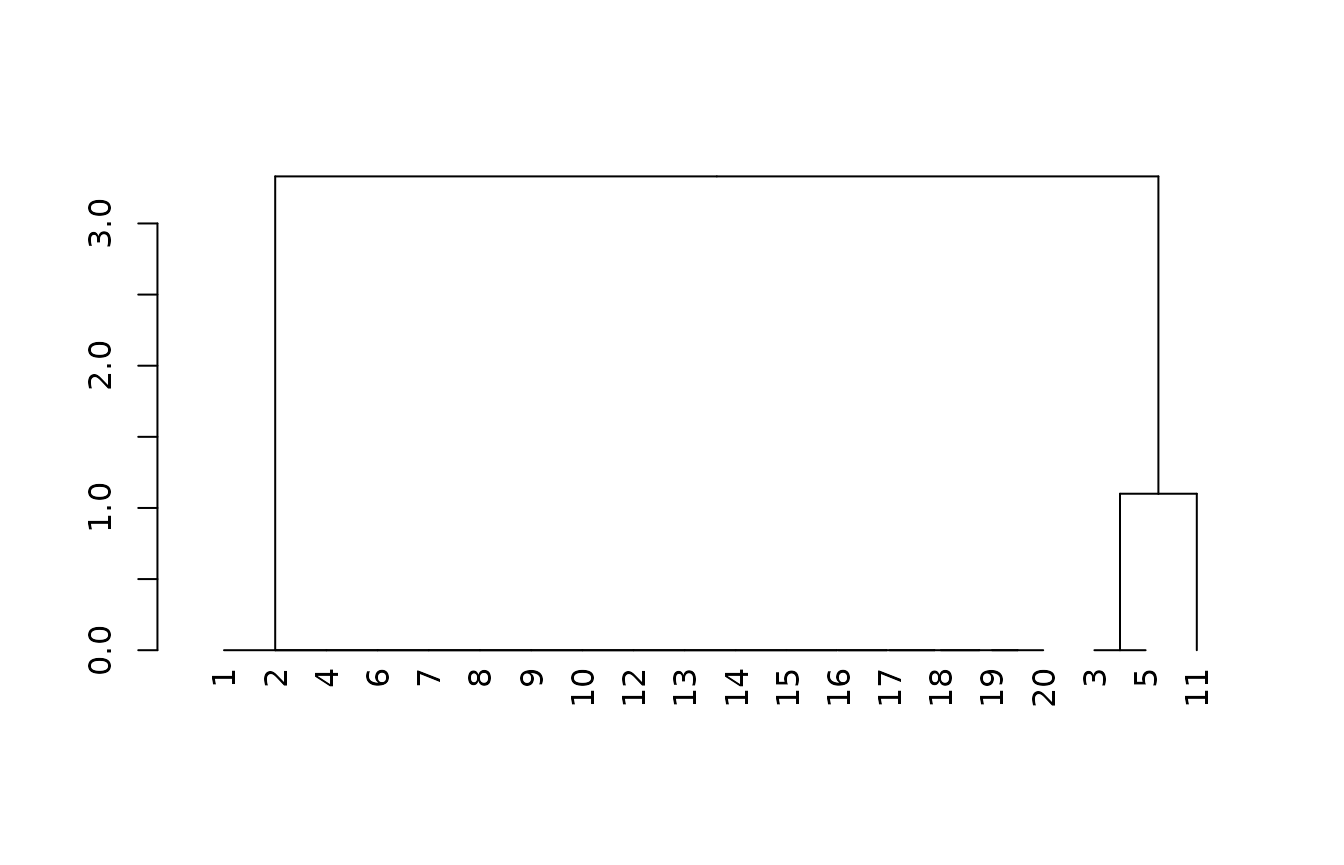

If we transform the particle size family, we have the option to combine similar classes, and also increase the taxonomic distance between other classes.

In this case, we code “fine-loamy” as a 4 and “loamy-skeletal” as a 7. The groups created by branching in the tree are identical to the simplest model, but the taxonomic distance between the two main groups of pedons is now greater (3 versus 1).

m1 <- cluster::agnes(x1[complete.cases(x1), ], method = "gaverage")
plot(as.dendrogram(m1))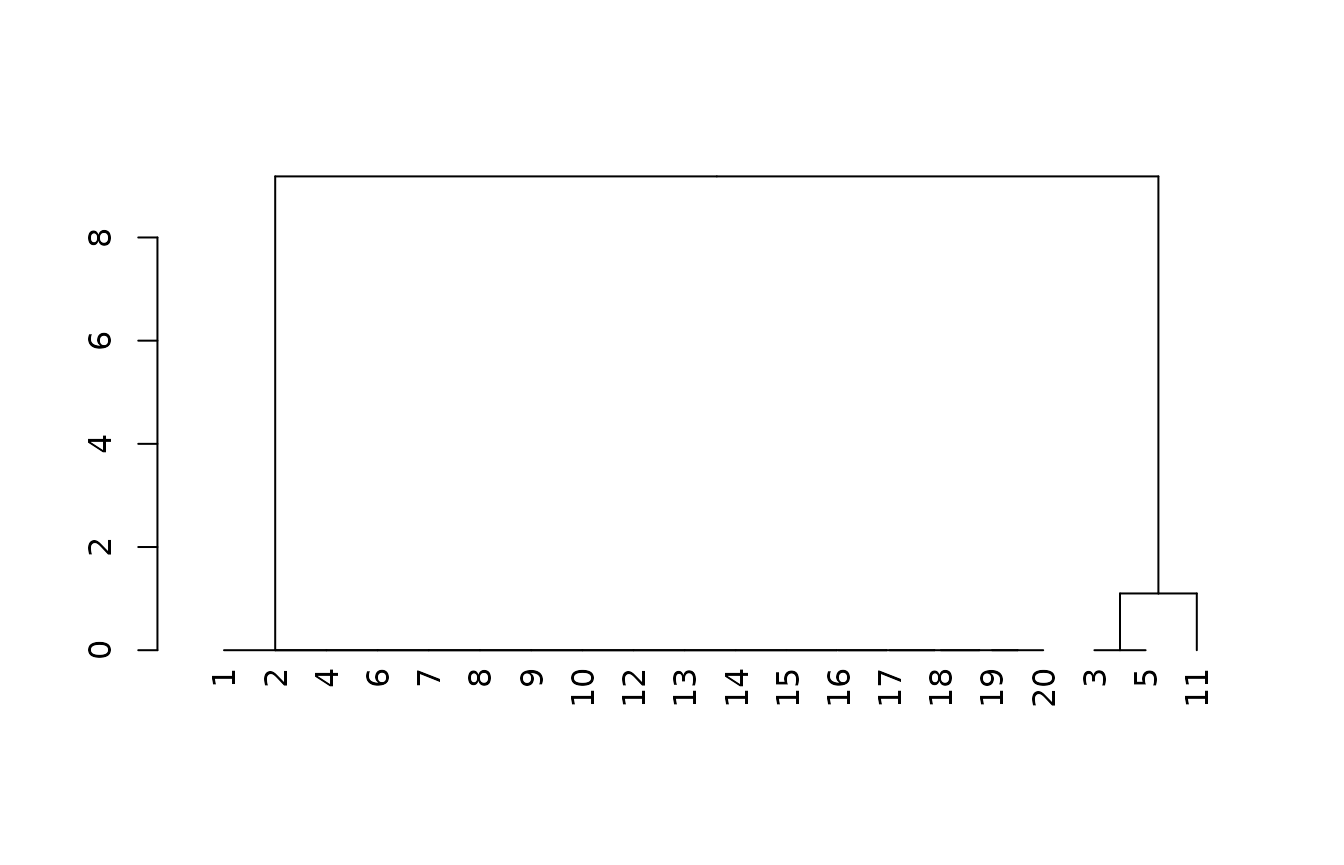

In the next most complex model we replace the taxonomic particle size class rating with the PSCS weighted average percent clay and the percent fragments.

We find the same outgroup of three pedons we separated earlier, the magnitude of taxonomic distances (y axis) further increases, and we get a lot more subtle variation within that reflects more continuous variation in PSCS clay and fragments.

m2 <- cluster::agnes(x2[complete.cases(x2),], method = "gaverage")
plot(as.dendrogram(m2))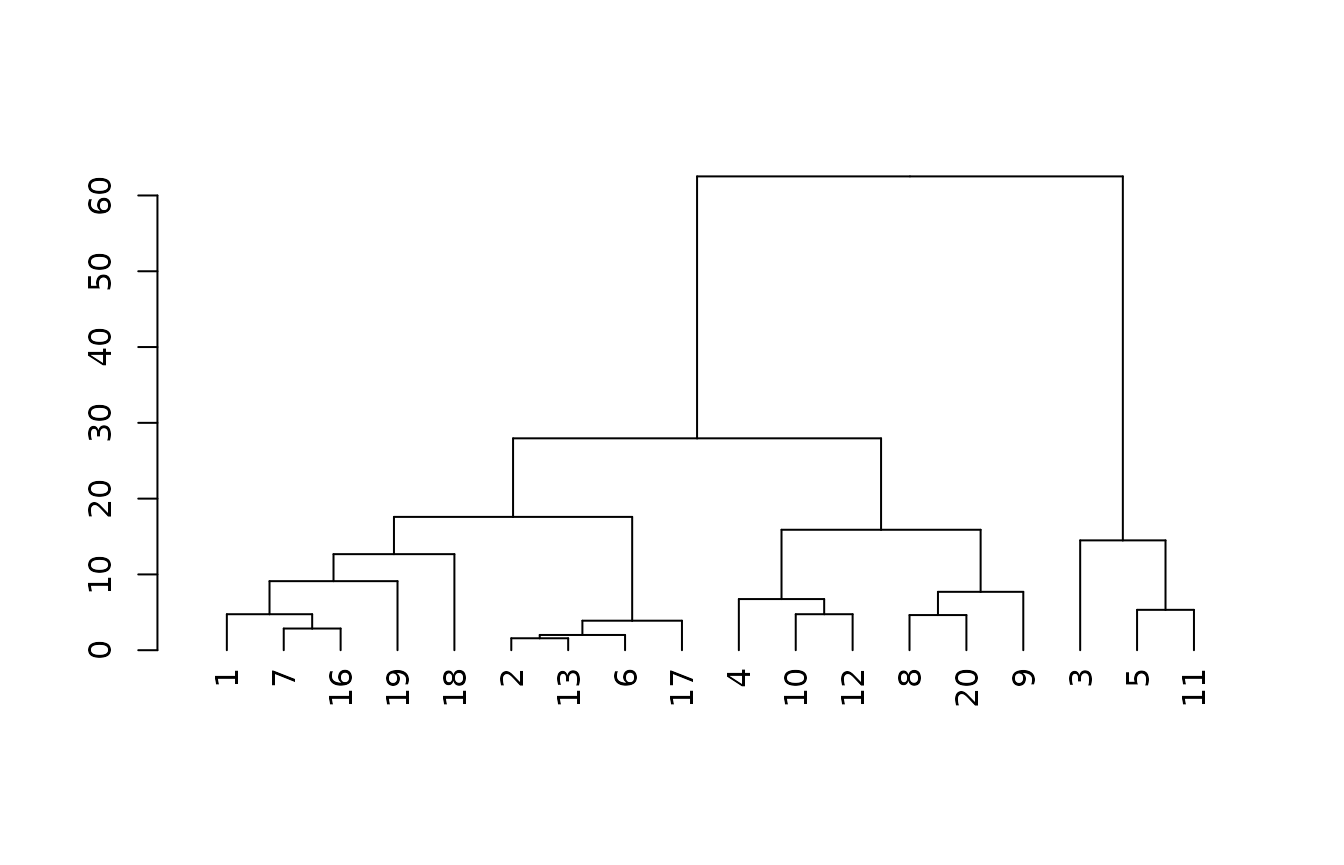

Since most of the soils in the loafercreek dataset are moderately deep we do not get much information from the depth class grouping. So, instead, in the next model we replace the depth class with the actual depth to root-limiting layer. We find again that the loamy-skeletal soils are separated, and some distances of groups within the fine-loamy soils shift, but ultimately there is little effect as the variation is still constrained within moderately deep depth class.

m3 <- cluster::agnes(x3[complete.cases(x3),], method = "gaverage")
plot(as.dendrogram(m3))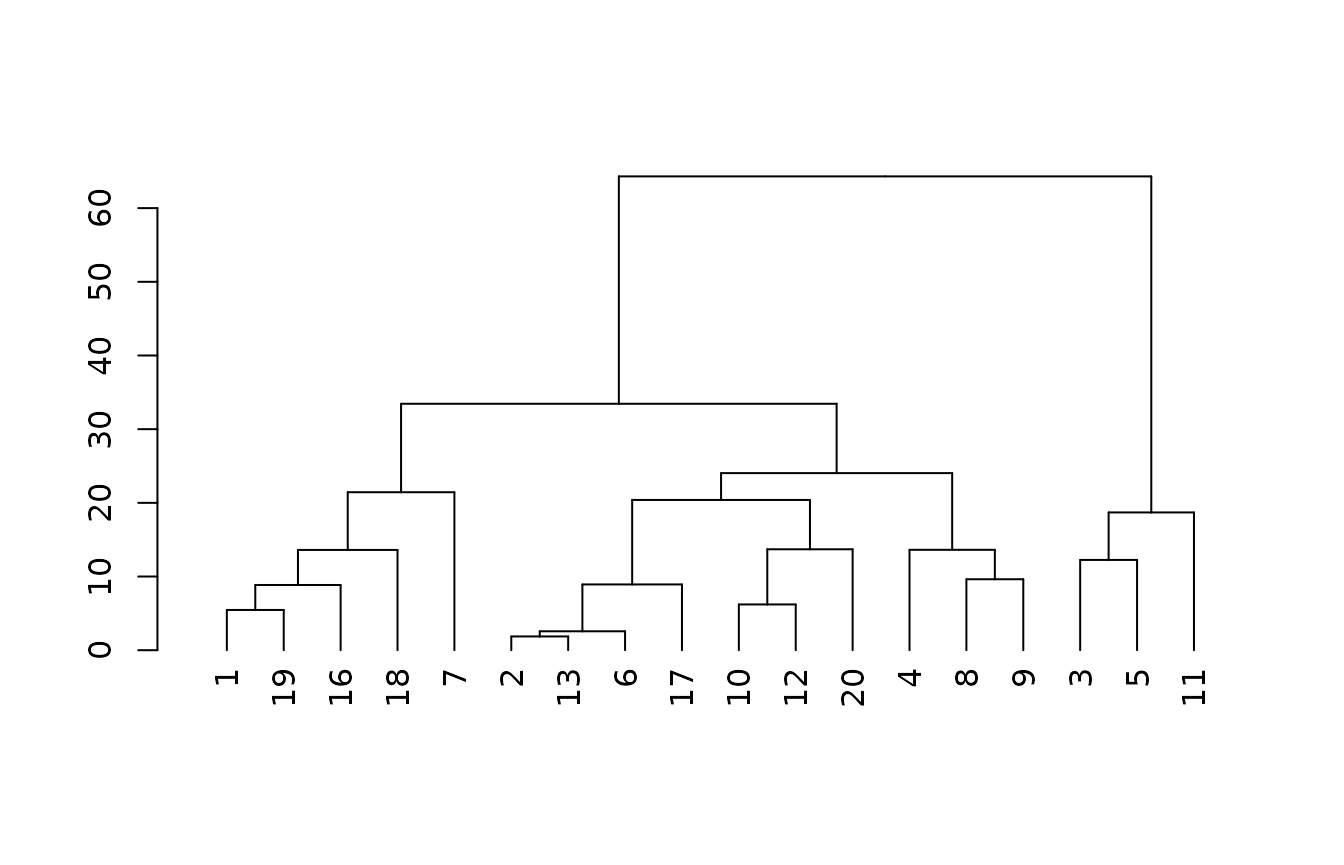

If we add the taxpartsize and depth class ratings back in with the continuous data we see that we get the exact same clustering as with the prior model (which included no categorical predictors). this indicates the categories are adequately covered by the numeric quantities we replaced them with.

m4 <- cluster::agnes(x4[complete.cases(x4),], method = "gaverage")
plot(as.dendrogram(m4))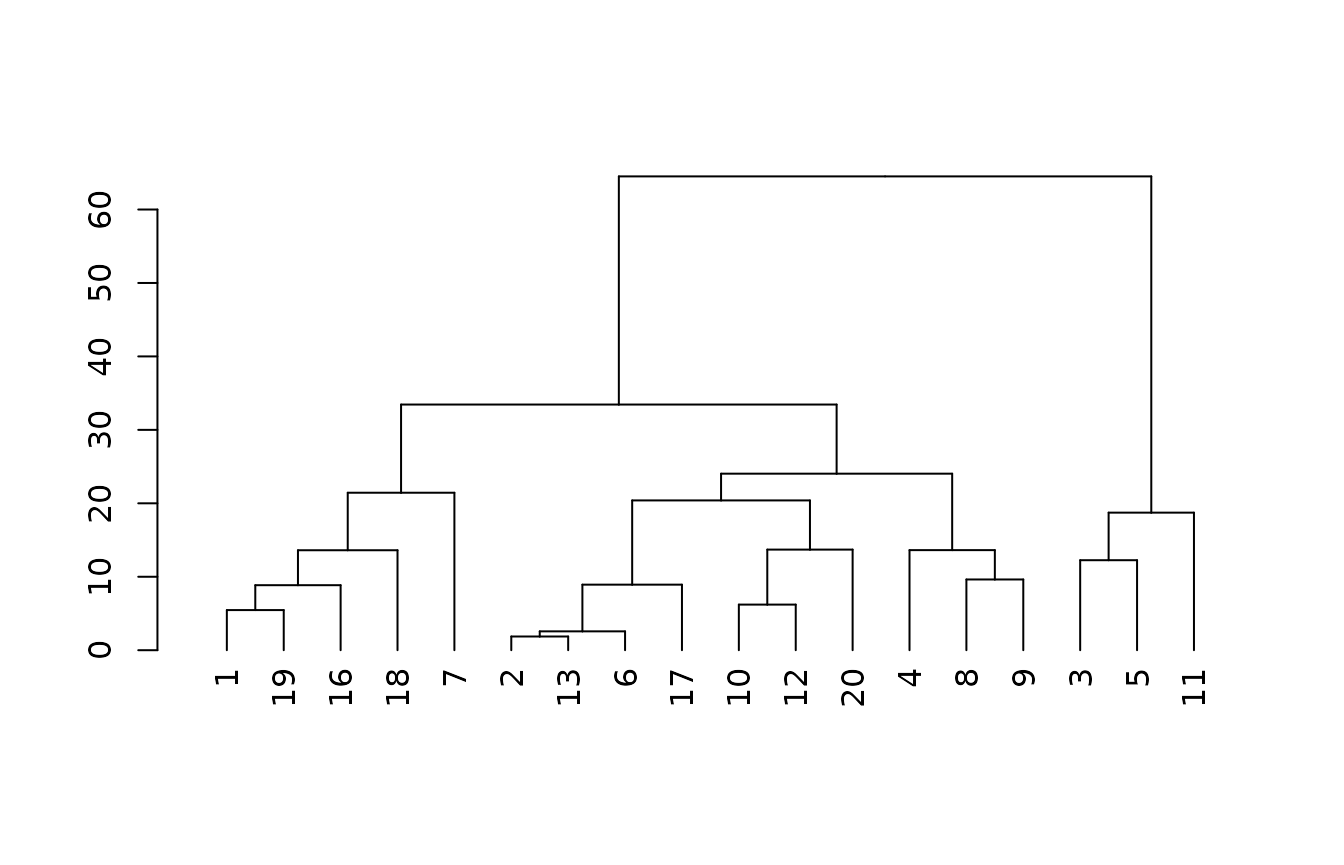

peiid	taxpartsize	rt	dp	rd	pc	pf
115595	fine-loamy	4	74	3	27.14000	4.60000
268820	fine-loamy	4	64	3	29.46000	15.76000
338023	loamy-skeletal	7	66	3	23.95652	65.26829
338040	fine-loamy	4	81	3	27.12500	26.25000
351716	loamy-skeletal	7	63	3	28.80000	54.42000
374205	fine-loamy	4	66	3	30.72000	17.36000
374219	fine-loamy	4	93	3	23.76000	6.64000
414936	fine-loamy	4	76	3	18.58000	27.98000
477059	fine-loamy	4	71	3	15.42000	20.38000
488573	fine-loamy	4	60	3	34.00000	30.00000
488596	loamy-skeletal	7	50	2	26.00000	50.00000
530694	fine-loamy	4	56	3	29.36842	31.05263
530751	fine-loamy	4	65	3	28.82000	17.20000
533172	fine-loamy	4	64	3	NaN	0.00000
533889	fine-loamy	4	61	3	NaN	15.00000
542125	fine-loamy	4	78	3	24.86000	9.28000
542131	fine-loamy	4	72	3	31.04000	13.56000
542154	fine-loamy	4	73	3	17.54167	0.00000
640616	fine-loamy	4	75	3	31.84000	2.00000
894145	fine-loamy	4	60	3	20.96000	24.00000

Here is a more complex example that adds maximum clay and fragments to the continuous variables included in the clustering.

It also provides code to compare divisive cluster::diana() and agglomerative (cluster::agnes()) hierarchical clustering methods as a method of visualizing “differences” based on a distance matrix.

To further enhance visualization of SoilProfileCollection objects, plotting of the associated distance matrices with sharpshootR::plotProfileDendrogram() is demonstrated.

# calculate some continuous quantities for PSCS
site(spc) <- site(mutate_profile(trunc(spc, spc$pscs_top, spc$pscs_bottom),
  mc = suppressWarnings(max(clay, na.rm=T)),
  mf = suppressWarnings(max(total_frags_pct, na.rm=T)))
)[c("peiid", "pc", "pf", "mc", "mf")]

spc <- spc[which(complete.cases(subset(site(spc), select=c("rt", "rd", "pc", "pf", "dp", "mc", "mf")))),]

# set up data frames for various clustering models
x0 <- subset(site(spc), select = c("taxpartsize", "rd"))
x1 <- subset(site(spc), select = c("rt", "rd"))
x2 <- subset(site(spc), select = c("pc", "pf", "rd"))
x3 <- subset(site(spc), select = c("pc", "pf", "dp"))
x4 <- subset(site(spc), select = c("rt", "rd", "pc", "pf", "dp"))
x5 <- subset(site(spc), select = c("rt", "rd", "pc", "pf", "dp", "mc", "mf"))

.clusterfun_hclust <- \(y, spc) {
  rownames(y) <- profile_id(spc)
  y[] <- lapply(y, \(z) if (is.character(z) || (!is.numeric(z))) factor(z) else z)
  stats::hclust(cluster::daisy(y[complete.cases(y),], metric = "gower"),
                method = "centroid")
}

.clusterfun_agnes <- \(y, spc) {
  rownames(y) <- profile_id(spc)
  y[] <- lapply(y, \(z) if (is.character(z) || (!is.numeric(z))) factor(z) else z)
  cluster::agnes(cluster::daisy(y[complete.cases(y),], metric = "gower"),
                 method = "gaverage")
}

.clusterfun_diana <- \(y, spc) {
  # NB: code ordinal factors beforehand if needed
  rownames(y) <- profile_id(spc)
  y[] <- lapply(y, \(z) if (is.character(z) || (!is.numeric(z))) factor(z) else z)
  cluster::diana(cluster::daisy(y, metric = "gower"))
}

# try the following code with the above thre clustering functions
.CLUSTERFUN <- .clusterfun_diana #.clusterfun_hclust #.clusterfun_agnes

# the simplest model uses the particle size family and the depth class
m0 <- .CLUSTERFUN(x0, spc)
#> Warning in cluster::daisy(y, metric = "gower"): binary variable(s) 2 treated as
#> interval scaled
sharpshootR::plotProfileDendrogram(spc, m0, name = NULL)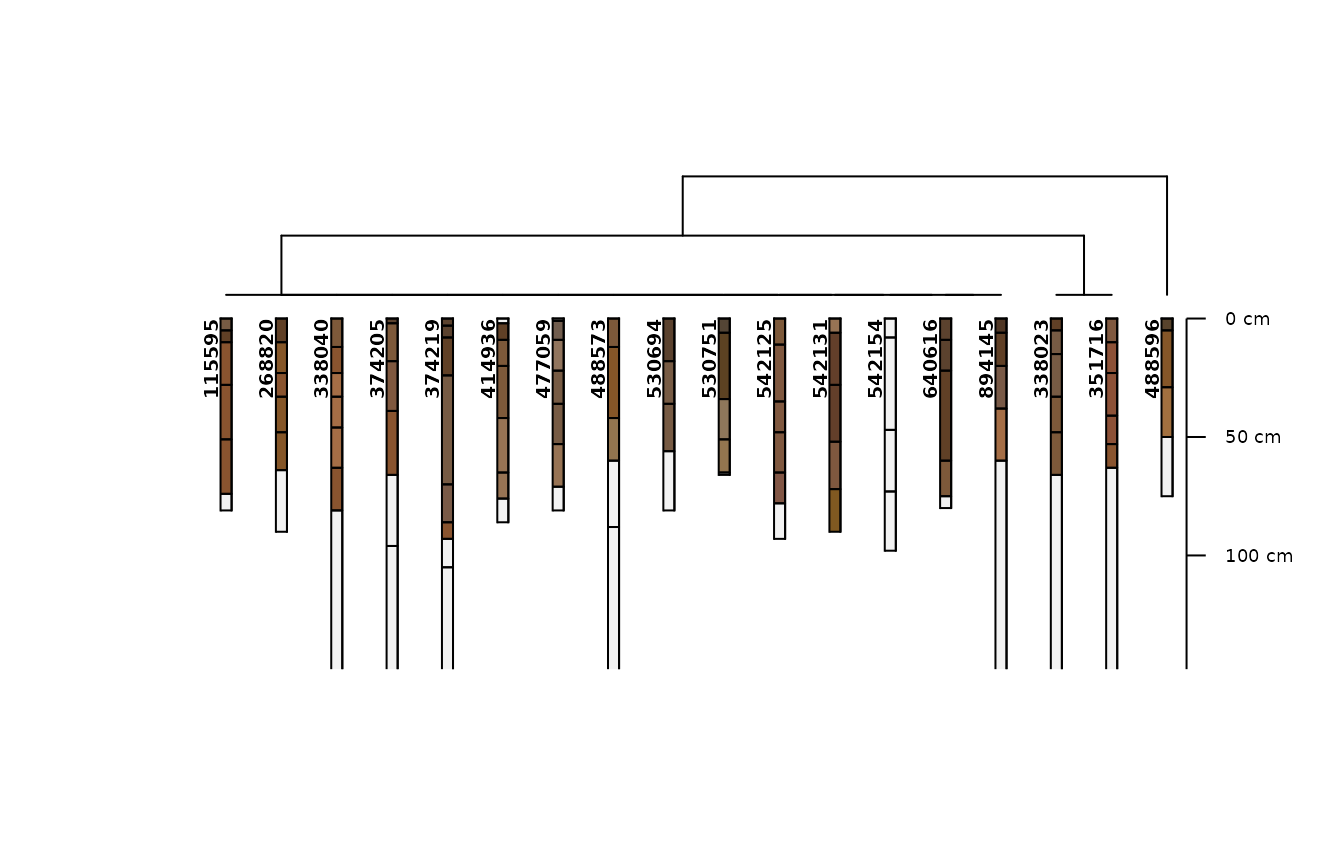
#
m1 <- .CLUSTERFUN(x1, spc)
#> Warning in cluster::daisy(y, metric = "gower"): binary variable(s) 1, 2 treated
#> as interval scaled
sharpshootR::plotProfileDendrogram(spc, m1, name = NULL)


m2 <- .CLUSTERFUN(x2, spc)
#> Warning in cluster::daisy(y, metric = "gower"): binary variable(s) 3 treated as
#> interval scaled
sharpshootR::plotProfileDendrogram(spc, m2, name = NULL)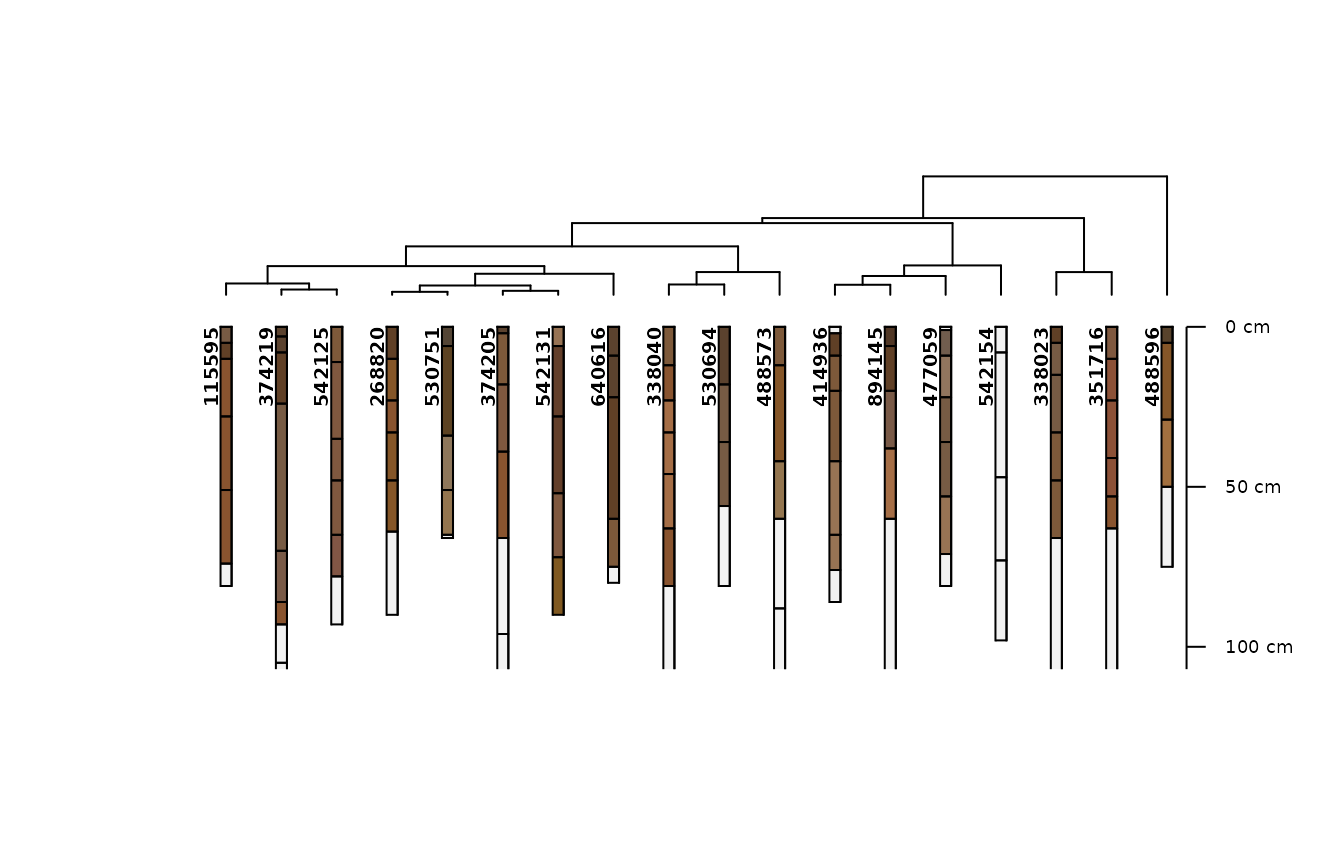


m3 <- .CLUSTERFUN(x3, spc)
sharpshootR::plotProfileDendrogram(spc, m3, name = NULL)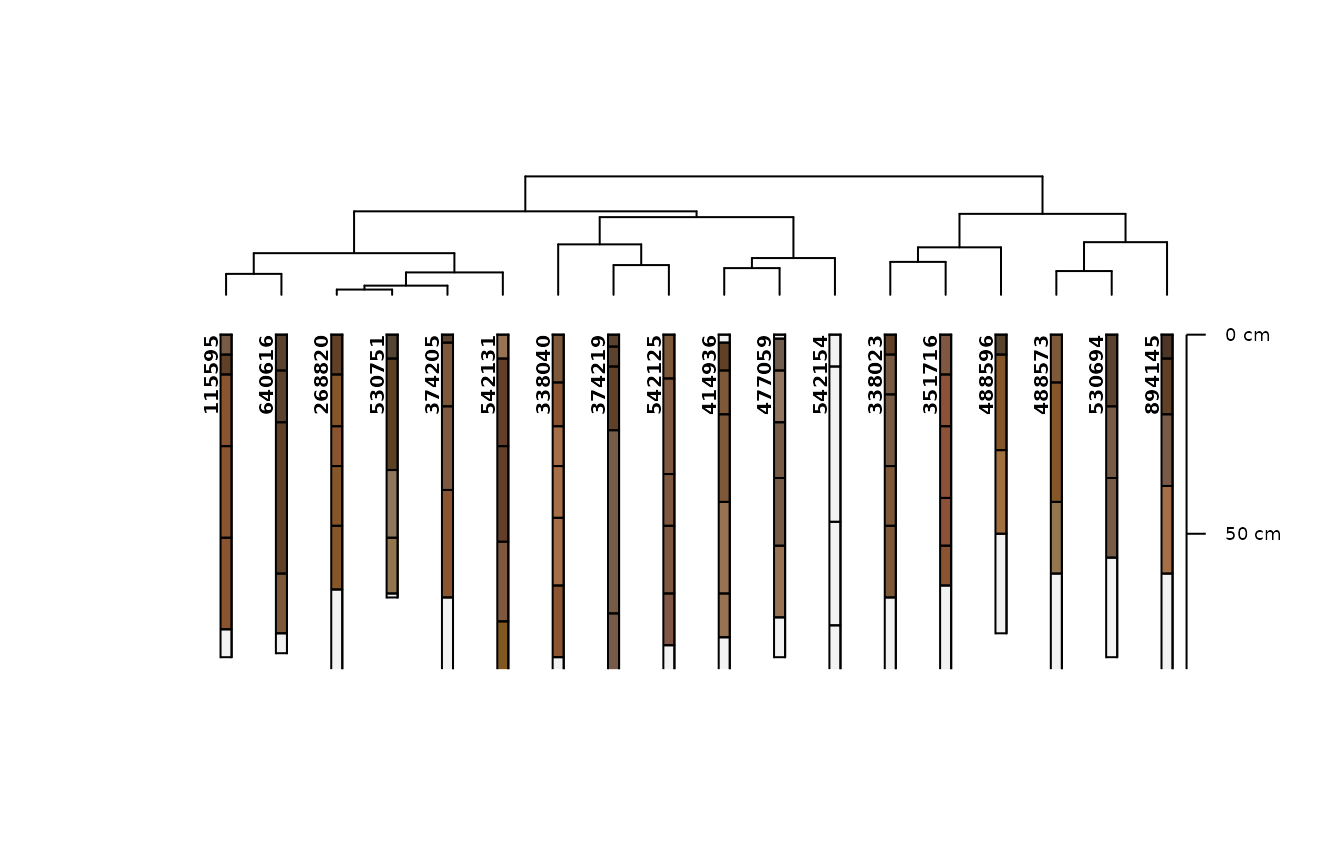

sharpshootR::plotProfileDendrogram() can also take most arguments you would supply to aqp::plotSPC().

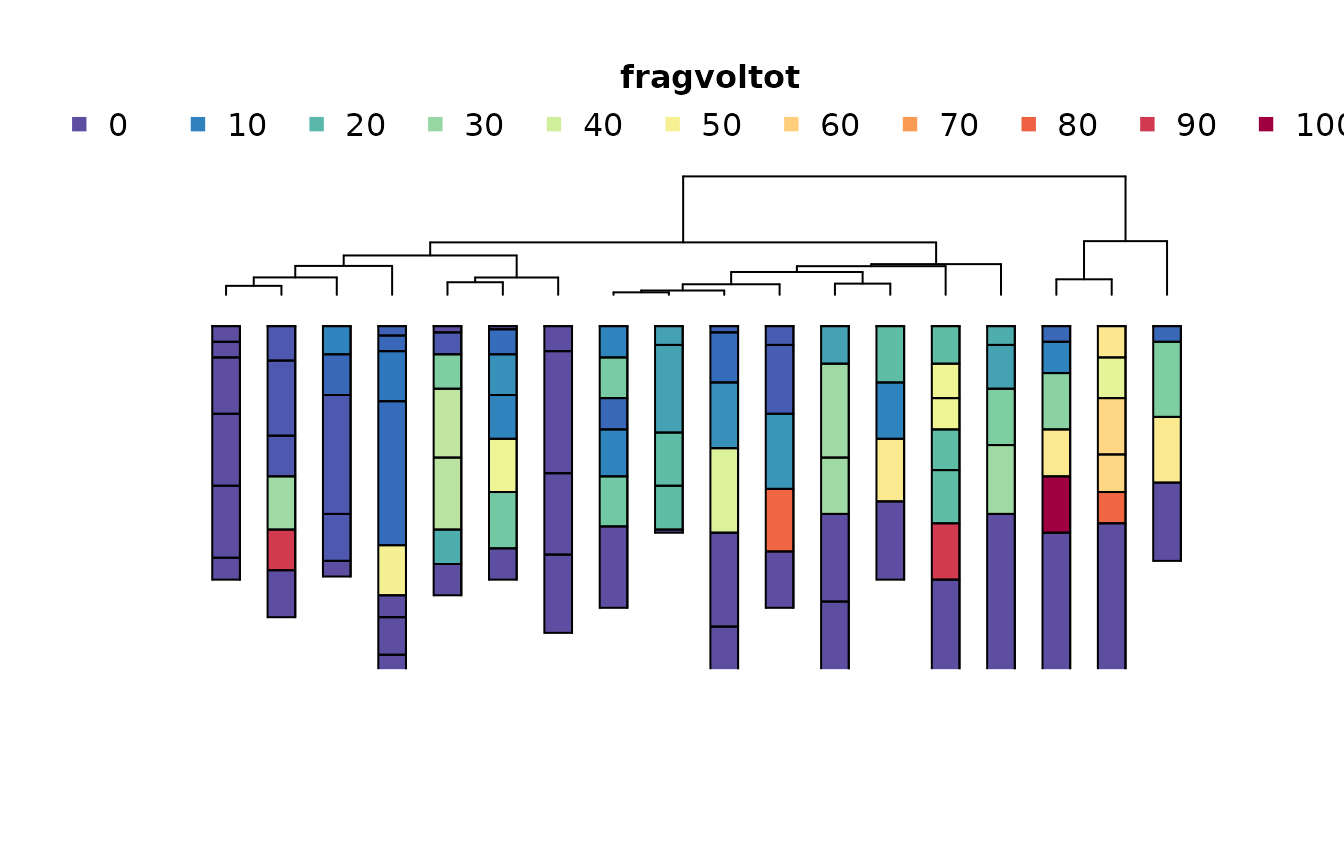
m4 <- .CLUSTERFUN(x4, spc)
#> Warning in cluster::daisy(y, metric = "gower"): binary variable(s) 1, 2 treated
#> as interval scaled
sharpshootR::plotProfileDendrogram(
  spc,
  m4,
  print.id = FALSE,
  name = NULL,
  depth.axis = FALSE,
  width = 0.25,
  color = "fragvoltot"
)


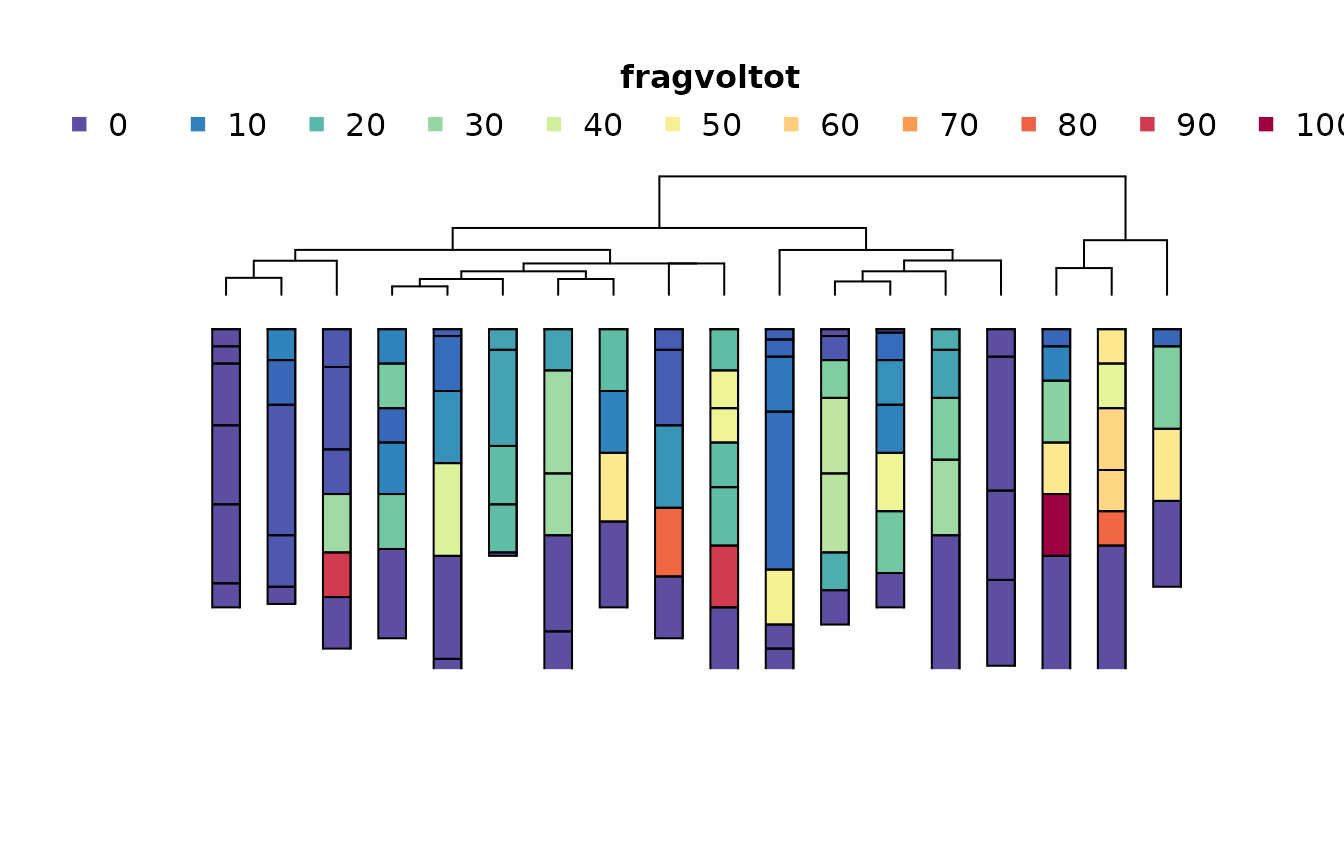
m5 <- .CLUSTERFUN(x5, spc)
#> Warning in cluster::daisy(y, metric = "gower"): binary variable(s) 1, 2 treated
#> as interval scaled
sharpshootR::plotProfileDendrogram(
  spc,
  m5,
  print.id = FALSE,
  name = NULL,
  depth.axis = NULL,
  width = 0.25,
  color = "fragvoltot"
)

peiid	taxpartsize	rt	dp	rd	pc	pf	mc	mf
115595	fine-loamy	4	74	3	27.14000	4.60000	35	5
268820	fine-loamy	4	64	3	29.46000	15.76000	38	24
338023	loamy-skeletal	7	66	3	23.95652	65.26829	25	95
338040	fine-loamy	4	81	3	27.12500	26.25000	30	45
351716	loamy-skeletal	7	63	3	28.80000	54.42000	35	75
374205	fine-loamy	4	66	3	30.72000	17.36000	39	40
374219	fine-loamy	4	93	3	23.76000	6.64000	26	8
414936	fine-loamy	4	76	3	18.58000	27.98000	20	35
477059	fine-loamy	4	71	3	15.42000	20.38000	19	45
488573	fine-loamy	4	60	3	34.00000	30.00000	34	30
488596	loamy-skeletal	7	50	2	26.00000	50.00000	26	50
530694	fine-loamy	4	56	3	29.36842	31.05263	36	50
530751	fine-loamy	4	65	3	28.82000	17.20000	31	20
542125	fine-loamy	4	78	3	24.86000	9.28000	30	30
542131	fine-loamy	4	72	3	31.04000	13.56000	37	75
542154	fine-loamy	4	73	3	17.54167	0.00000	18	0
640616	fine-loamy	4	75	3	31.84000	2.00000	44	2
894145	fine-loamy	4	60	3	20.96000	24.00000	24	30